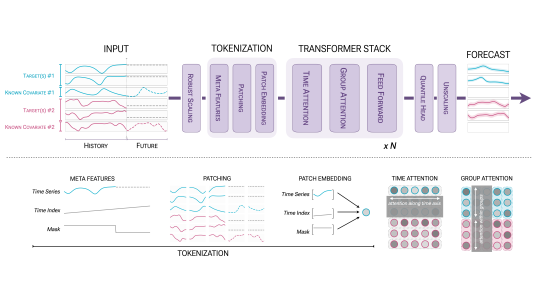
Deep learning’s transformative impact has become widely evident with the advent and rapid adoption of large language models (LLMs). LLMs and other so-called foundation models are potentially powerful tools for advancing a wide range of both pure and applied sciences. However, despite the role foundation models have played in language and computer vision, there has been a slower rate of adoption in scientific domains, such as computational fluid dynamics (CFD). This raises a question: what would it take for deep-learning foundation models to play a more significant role in scientific applications?
We explored a similar idea in 2023 when we observed that deep-learning (DL) methods had “shown promise for scientific computing, where they can be used to predict solutions to partial differential equations (PDEs)” but required hard constraints for physically meaningful predictions. A year later, at ICLR 2024, we hosted a workshop aimed at bridging the gap between scientists interested in using machine learning (ML) to solve real-world problems and ML researchers who have attempted to apply ML methods to scientific problems but require more real-world test cases.

In this post, I'll explore potential applications of foundation models (FMs) for probabilistic time series forecasting for both univariate (one-dimensional) and spatiotemporal (two- and three-dimensional) data in scientific domains. In addition, I'll describe critical differences between LLMs and scientific foundation models, including a scarcity of available training data; the vital importance of strict adherence to physical laws; and the role of uncertainty quantification in robust decision making.
Probabilistic time series forecasting
We begin with univariate time series forecasting prediction, which has applications ranging from retail demand forecasting to scientific predictions. Here our task is to predict the future time points given the historical data and covariates. With probabilistic time series forecasting, we aim to provide a distribution of future points conditioned on these past observations.
Traditional or local statistical methods, which are designed to fit a separate model for each individual time series (e.g., autoregressive integrated moving average and exponential smoothing) have been widely utilized. More recently, we’ve seen a rise in global DL models trained across a large amount of related time series, including DeepAR and MQ-CNN/MQ-Transformer. But can we push this further and propose a foundation model for time series forecasting?
Inspired by the success of LLMs, last year we presented the time series foundation model (TSFM) Chronos, which aims to answer the question "Can an out-of-the-box language model be applied to time series?" Chronos treats every historical data point as a token and uses a T5 language model as a generative model to perform the next-token prediction, continuing autoregressively. Chronos significantly outperformed both classical statistical methods and specialized deep-learning models directly trained on individual datasets.
While Chronos used a language-modeling framework, some key distinctions remain between time series and language data. These include significantly less available pretraining data for time series relative to language data, how to represent continuous time series data as discrete tokens, and the frequency of time series data.
To deal with the data discrepancy, we relied on synthetic pretraining data for Chronos. We increased the amount of that data by applying a TSMix method that mixes time series of different frequencies while also relying on synthetic data generated from Gaussian processes. These techniques enhanced model robustness and generalization.
Another key challenge in designing a TSFM is how to map continuous time series data to discrete tokens as inputs to the LLM. There are various strategies for embedding continuous dynamics as discrete tokens. Chronos achieves this via simple binning or quantization as well as wavelet tokenization, whereas Chronos-Bolt utilizes continuous embeddings.
An interesting, and somewhat surprising, lesson has arisen here. While Chronos-Bolt and other follow-ups incorporated more classical forecasting methodology, leading to better performances on classical time series benchmark datasets, the original LLM-based Chronos has the strongest performance on chaotic and dynamical system datasets. This may be unexpected since Chronos was not designed for chaotic systems and does not use any such data in its pretraining process. The result owes to the intrinsic capability of Chronos to parrot or mimic past history without regressing to the mean, as classical time series methods or other TSFMs do. Chronos has already found wide applications in the sciences, including in water, energy, and traffic forecasting.
Spatiotemporal forecasting
Unlike univariate temporal forecasting, spatiotemporal forecasting entails predicting future points that include both space and time dimensions. This kind of forecasting is important in CFD, weather forecasting, and even the prediction of earthquake aftershocks.
Traditionally, spatiotemporal dynamics for CFD have been solved by numerical methods, including finite-difference, finite-volume, and finite-element methods. These methods have long powered the solvers for PDEs, which are the physical equations (e.g., the Navier-Stokes equations) that govern fluid dynamics. Recently, DL models have shown promise, especially for short-term weather forecasting and aerodynamics.
Weather forecasting
Progress in the development of deep-learning weather prediction (DLWP) models has advanced to the point where they rival traditional numerical weather prediction (NWP) models. This owes in part to an abundance of real-world data, including the ERA5 dataset. The recent surge of DLWPs raises the question of which approach is most suitable.
That inspired us to compare and contrast the most prominent backbones used in DLWP models. We were the first to conduct a controlled study with the same parameter count, training protocol, and set of input variables for each DLWP model on both two-dimensional incompressible Navier-Stokes dynamics with various Reynolds numbers and on the real-world WeatherBench dataset.
We find tradeoffs in terms of accuracy and memory consumption. For example, on the WeatherBench dataset, we show SwinTransformer to be effective for short- to medium-ranged forecasts. Importantly, for long-ranged weather rollouts of up to one year, we observe stability and physical soundness in architectures that formulate a spherical data representation of the globe, i.e., the graph-neural-network-based GraphCast and Spherical FNO.
While DLWP models are powerful, a perhaps surprising finding is that as we increase the number of parameters, these models tend to saturate and do not satisfy the neural scaling laws that LLMs do.
Aerodynamics
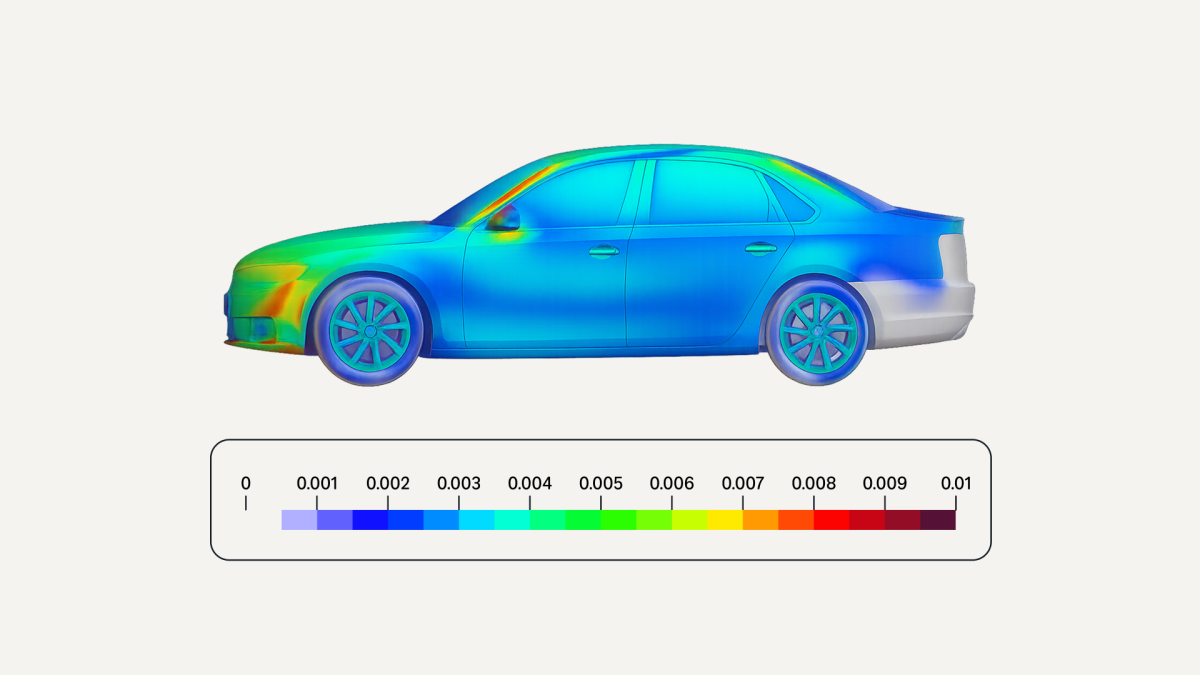
Recently, DL models have been investigated as a way to speed up simulations in areas where traditional numerical solvers are computationally expensive (approximating 3-D spatiotemporal data with high accuracy requires fine meshes). Even assuming a slight loss of accuracy relative to traditional solvers, DL models can be helpful in an iterative design process. For example, a fast approximation of flows can help engineers quickly test and iterate through several different car geometries or airplane designs.
The theme of data scarcity resurfaces here as well. Generating relevant training data is extremely expensive since it requires running numerical solvers. We have released high fidelity 3-D datasets, including DrivAerML, WindsorML, and AhmedML. These open datasets have already proven valuable: EmmiAI used them as critical components in building their FMs for automotive dynamics.
Such datasets are vital for improved generalization in scientific domains where there is a deficiency of data. That need is widespread, which underscores the importance of abundant synthetic data, particularly in applications that represent different physics from various PDEs, boundary conditions, and geometries.
Physical constraints and uncertainty quantification
Violations of physical constraints and deterministic predictions also limit the widespread adoption of DL and foundation models. DL models have been shown to violate known physical laws, e.g., conservation of mass, energy, and momentum, and known boundary conditions, e.g., allowing heat flux across an insulator.
Enforcing these constraints can lead to physically accurate solutions and guide the learning process to result in more accurate predictions. For instance, in the challenging case of two-phase flow problems, e.g., modeling the moving interface between air and water, our ProbConserv model, which enforces the conservation law, improves prediction accuracy, shock location detection, and out-of-domain performance.
Our initial research, which considered linear constraints, has also been extended to handle nonlinear constraints through a differentiable probabilistic projection framework. Our methodology can be used to enforce a wide range of constraints in various domains, including conservation law constraints in PDEs and coherency constraints in hierarchical time series forecasting.
We can also enforce physical constraints on generative models, e.g., diffusion or functional flow-matching models (FFMs) to guarantee physically meaningful generations. For instance, our latent diffusion model for precipitation nowcasting, PreDiff, incorporates physical knowledge as a soft constraint using a type of knowledge alignment: a lower probability is assigned to the less physical samples in the denoising generative process. Our FFM-based ECI sampling outputs generations of various PDEs that are guaranteed to satisfy known initial and boundary conditions and conservation laws by using a projection method similar to ProbConserv.
Another important property of these methods is that they provide uncertainty quantification (UQ) and probabilistic predictions, which are critical in scientific and safety-critical domains and for corresponding downstream tasks. For example, PreDiff inherently provides UQ, which results in higher resolution and sharper predictions than deterministic approaches. In ProbConserv, we also use the variance of the unconstrained model to update the solution the most, according to the constraint, in the region where the variance or uncertainty is the largest.
Conclusion
In conclusion, in order for FMs to achieve widespread adoption, ensuring reliable physical-constraint satisfaction and robust uncertainty quantification are essential to gain trust from domain scientists. With interdisciplinary collaborations between scientists and ML experts, the potential growth of these models is limitless.
Acknowledgments: Thank you to Bernie Wang, Michael W. Mahoney, Fatir Abdul Ansari, Boran Han, Xiyuan Zhang and Annan Yu.