For centuries, theories of meaning have been of interest almost exclusively to philosophers, debated in seminar rooms and at conferences for small specialty audiences.
But the advent of large language models (LLMs) and other “foundation models” has changed that. Suddenly, mainstream media are alive with speculation about whether models trained only to predict the next word in a sequence can truly understand the world.

Skepticism naturally arises. How can a machine that generates language in such a mechanical way grasp words’ meanings? Simply processing text, however fluently, would not seem to imply any sort of deeper understanding.
This kind of skepticism has a long history. In 1980, the philosopher John Searle proposed a thought experiment known as the Chinese room, in which a person who does not know Chinese follows a set of rules to manipulate Chinese characters, producing Chinese responses to Chinese questions. The experiment is meant to show that, since the person in the room never understands the language, symbolic manipulation alone cannot lead to semantic understanding.
Similarly, today’s critics often argue that since LLMs are able only to process “form” — symbols or words — they cannot in principle achieve understanding. Meaning depends on relations between form (linguistic expressions, or sequences of tokens in a language model) and something external, these critics argue, and models trained only on form learn nothing about those relations.
But is that true? In this essay, we will argue that language models not only can but do represent meanings.
Probability space
At Amazon Web Services (AWS), we have been investigating concrete ways to characterize meaning as represented by LLMs. The first challenge with these models is that there is no clear candidate for “where” meanings could reside. Today’s LLMs are usually decoder-only models; unlike encoder-only or encoder-decoder models, they do not use a vector space to represent data. Instead, they represent words in a distributed way, across the many layers and attention heads of a transformer model. How should we think of meaning representation in such models?
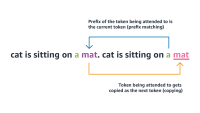
In our paper “Meaning representations from trajectories in autoregressive models”, we propose an answer to this question. For a given sentence, we consider the probability distribution over all possible sequences of tokens that can follow it, and the set of all such distributions defines a representational space.
To the extent that two sentences have similar continuation probabilities — or trajectories — they’re closer together in the representational space; to the extent that their probability distributions differ, they’re farther apart. Sentences that produce the same distribution of continuations are “equivalent”, and together, they define an equivalence class. A sentence’s meaning representation is then the equivalence class that it belongs to.

In the field of natural-language processing (NLP), it is widely recognized that the distribution of words in language is closely related to their meaning. This idea is known as the “distributional hypothesis” and is often invoked in the context of methods like word2vec embeddings, which build meaning representations from statistics on word co-occurrence. But we believe we are the first to use the distributions themselves as the primary way to represent meaning. This is possible since LLMs offer a way to evaluate these distributions computationally.
Of course, the possible continuations of a single sentence are effectively infinite, so even using an LLM we can never completely describe their distribution. But this impossibility reflects the fundamental indeterminacy of meaning, which holds for people and AI models alike. Meanings are not directly observed: they are encoded in the billions of synapses in a brain or the billions of activations of a trained model, which can be used to produce expressions. Any finite number of expressions may be compatible with multiple (indeed, infinitely many) meanings; which meaning the human — or the language model — intends to convey can never be known for sure.
What is surprising, however, is that, despite the large dimensionality of today’s models, we do not need to sample billions or trillions of trajectories in order to characterize a meaning. A handful — say, 10 or 20 — is sufficient. Again, this is consistent with human linguistic practice. A teacher asked what a particular statement means will typically rephrase it in a few ways, in what could be described as an attempt to identify the equivalence class to which the statement belongs.
In experiments reported in our paper, we showed that a measure of sentence similarity that uses off-the-shelf LLMs to sample token trajectories largely agrees with human annotations. In fact, our strategy outperforms all competing approaches on zero-shot benchmarks for semantic textual similarity (STS).
Form and content
Does this suggest that our paper’s definition of meaning — a distribution over possible trajectories — reflects what humans do when they ascribe meaning? Again, skeptics would say that it couldn’t possibly: text continuations are based only on “form” and lack the external grounding necessary for meaning.
But probabilities over continuations may capture something deeper about how we interpret the world. Consider a sentence that begins “On top of the dresser stood … ” and the probabilities of three possible continuations of that sentence: (1) “a photo”; (2) “an Oscar statuette”; and (3) “an ingot of plutonium”. Don’t those probabilities tell you something about what, in fact, you can expect to find on top of someone’s dresser? The probabilities over all possible sentence continuations might be a good guide to the likelihood of finding different objects on the tops of dressers; in that case, the “formal” patterns encoded by the LLM would tell you something particular about the world.
The skeptic might reply, however, that it’s the mapping of words to objects that gives the words meaning, and the mapping isn’t intrinsic to the words themselves; it requires human interpretation or some other mechanism external to the LLM.
But how do humans do that mapping? What happens inside you when you read the phrase “the objects on top of the dresser”? Maybe you envision something that feels somehow indefinite — a superposition of the dresser viewed from multiple angles or heights, say, with abstract objects in a certain range of sizes and colors on top. Maybe you also envision the possible locations of the dresser in the room, the room’s other furnishings, the feel of the wood of the dresser, the scent of the dresser or of the objects on top of it, and so on.
All of those possibilities can be captured by probability distributions, over data in multiple sensory modalities and in multiple conceptual schemas. So maybe meaning for humans involves probabilities over continuations, too, but in a multisensory space instead of a textual space. And on that view, when an LLM computes continuations of token sequences, it’s accessing meaning in a way that resembles what humans do, just in a more limited space.
Skeptics might argue that the passage from the multisensory realm to written language is a bottleneck that meaning can’t squeeze through. But that passage could also be interpreted as a simple projection, similar to the projection from a three-dimensional scene down to a two-dimensional image. The two-dimensional image provides only partial information, but in many situations, the scene remains quite understandable. And since language is our main tool for communicating our multisensory experiences, the projection into text might not be that "lossy" after all.
This is not to say that today’s LLMs grasp meanings in the same way that humans do. Our work shows only that large language models develop internal representations with semantic value. We’ve also found evidence that such representations are composed of discrete entities, which relate to each other in complex ways — not just proximity but directionality, entailment, and containment.
But those structural relationships may differ from the structural relationships in the languages used to train the models. That would remain true even if we trained the model on sensory signals: we cannot directly see what meaning subtends a particular expression, for a model any more than for a human.
If the model and human have been exposed to similar data, however, and if they have shared enough experiences (today, annotation is the medium of sharing), then there is a basis on which to communicate. Alignment can then be seen as the process of translating between the model’s emergent “inner language” — we call it “neuralese” — and natural language.
How faithful can that alignment be? As we continue to improve these models, we will need to face the fact that even humans lack a stable, universal system of shared meanings. LLMs, with their distinct approach to processing information, may simply be another voice in a diverse chorus of interpretations.
In one form or another, questions about the relationship between the world and its representation have been central to philosophy for at least 400 years, and no definitive answers have emerged. As we move toward a future in which LLMs are likely to play a larger and larger role, we should not dismiss ideas based only on our intuitions but continue to ask these difficult questions. The apparent limitations of LLMs might be only a reflection of our poor understanding of what meaning actually is.