Automated reasoning is the algorithmic search through the infinite set of theorems in mathematical logic. We can use automated reasoning to answer questions about what systems such as biological models and computer programs can and cannot do in the wild.
In the 1990s, AMD, IBM, Intel, and other companies invested in automated reasoning for circuit and microprocessor design, leading to today’s widely used and industry-standard hardware formal-verification tools (e.g., JasperGold). In the 2000s, automated reasoning expanded to niche software domains such as device drivers (e.g., Static Driver Verifier) or transportation systems (e.g., Prover technology). In the 2010s, we saw automated reasoning increasingly applied to our foundational computing infrastructure, such as cryptography, networking, storage, and virtualization.
With recently launched cloud services such as IAM Access Analyzer and VPC Network Access Analyzer, automated reasoning is now beginning to change how computer systems built on top of the cloud are developed and operated.
All these applications of automated reasoning rest on a common foundation: automated and semi-automated mechanical theorem provers. ACL2, CVC5, HOL-light’s Meson_tac, MiniSat, and Vampire are a few examples, but there are many more we could name. They are all, in outline, working on the same problem: the search for proofs in mathematical logic.
Over the past 30 years, slowly but surely, a virtuous cycle has formed: automated reasoning in specific and critical application areas drives more investment in foundational tools, while improvements in the foundational tools drive further applications. Around and around.
The increasingly difficult benchmarks driving the development of these tools present new science opportunities. International competitions such as CASC, SAT-COMP, SMT-COMP, SV-COMP, and the Termination competition have accelerated this virtuous cycle. On the application side, with increasing power from the tools come new research opportunities in the design of customer-intuitive tools (such as models of cellular signaling pathways or Amazon's abstraction of control policies for cloud computing).
As an example of the virtuous cycle at work, consider the following graph, which shows the results for all of the winners of SAT-COMP from 2002 to 2021, compared apples-to-apples in a competition with the same hardware and same benchmarks:
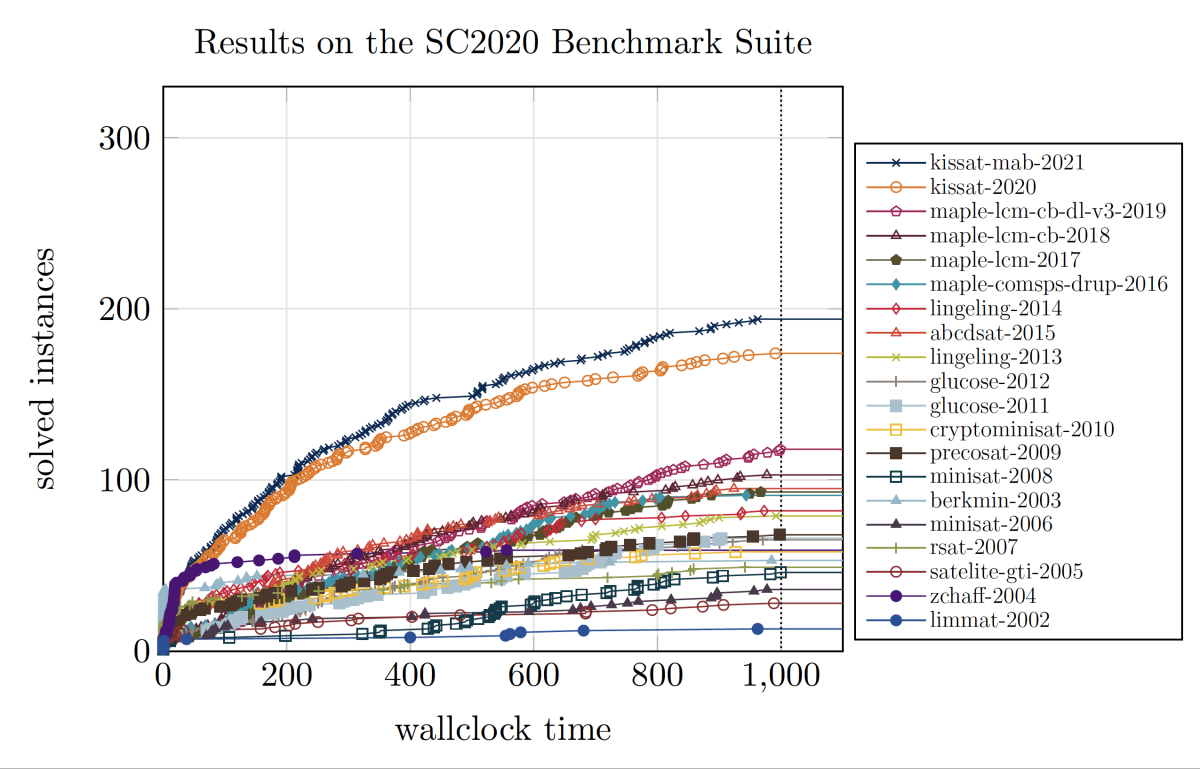
This graph plots the number of benchmarks that each solver can solve in 200 seconds, 400 seconds, etc. The higher the line, the more benchmarks the solver could solve. By looking at the plot we can see, for example, that the 2010 winner (cryptominisat) solved approximately 50 benchmarks within the allotted 1,000 seconds, whereas the 2021 winner (kissat) can solve nearly four times as many benchmarks in the same time, using the same hardware. Why did the tools get better? Because members of the scientific community pushing on the application submitted benchmarks to the competitions, which helped tool developers take the tools to new heights of performance and scale.
At Amazon we see the velocity of the virtuous cycle dramatically increasing. Our automated-reasoning tools are now called billions of times daily, with growth rates exceeding 100% year-over-year. For example, AWS customers now have access to automated-reasoning-based features such as IAM Access Analyzer, S3 Block Public Access, or VPC Reachability Analyzer. We also see Amazon development teams using tools such as Dafny, P, and SAW.
What’s most exciting to me as an automated-reasoning scientist is that our research area seems to be entering a golden era. I think we are beginning to witness a transformation in automated reasoning that is similar to what happened in virtualized computing as the cloud’s virtuous cycle spun up. As described in Werner Vogels’s 2019 re:Invent keynote, AWS’s EC2 team was driven by unprecedented customer adoption to reinvent its hypervisor, microprocessor, and networking stack, capturing significant improvements in security, cost, and team agility made possible by economies of scale.
There are parallels in automated reasoning today. Dramatic new infrastructure is needed for viable business reasons, putting a spotlight on research questions that were previously obscure and unsolved. Below I outline three examples of open research areas driven by the increasing scale of automated-reasoning tools and our underlying computing infrastructure.
Example: Distributed proof search
For over two decades the automated-reasoning scientific community has postulated that distributed-systems-based proof search could be faster than sequential proof search. But we didn’t have the economic scale to justify serious investigation of the question.
At Amazon, with our increased reliance on automated reasoning, we now have that kind of scale. For example, we sponsored the new cloud-based-tool tracks in several international competitions.
Compare the mallob-mono solver, the winner of SAT-COMP’s new cloud-solver track, to the single-microprocessor solvers:
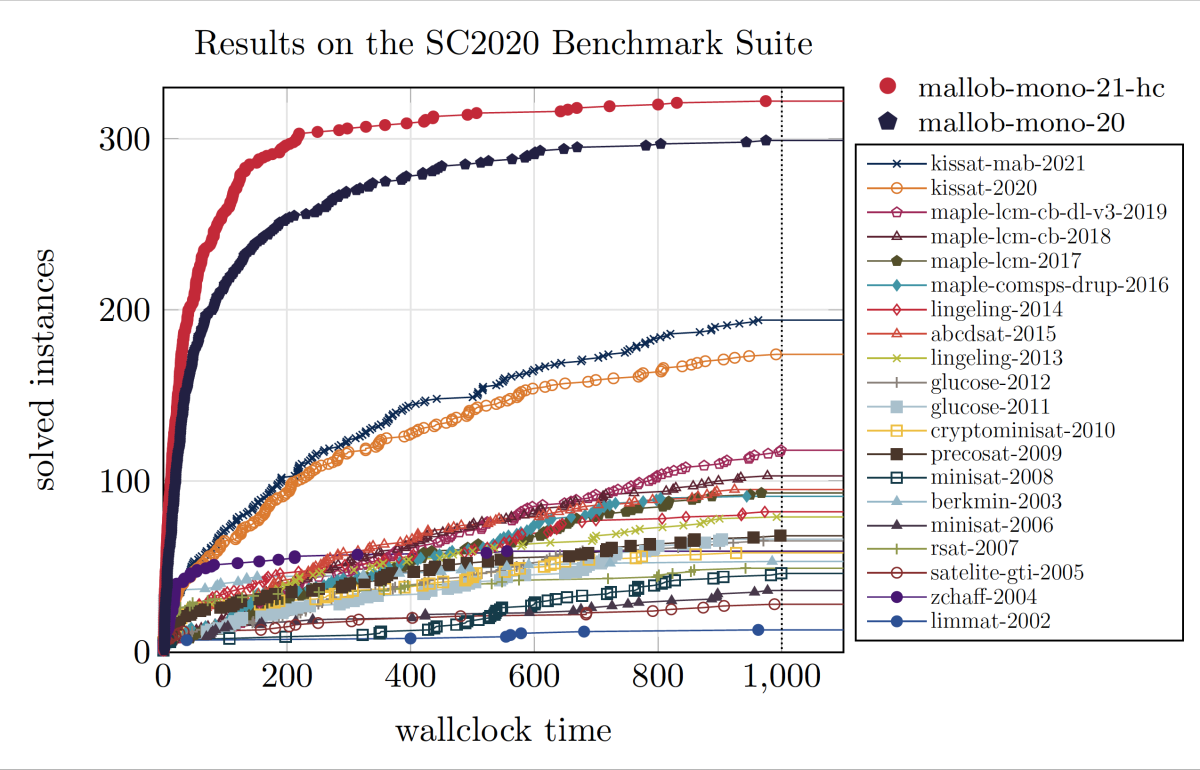
Mallob-mono is now, by a wide margin, the most powerful SAT solver on the planet. And like the sequential solvers, the distributed solvers are improving.
As described in Kuhn’s seminal book The Structure of Scientific Revolutions, major perspective shifts like this tend to trigger scientific revolutions. The success of distributed proof search raises the possibility of similar revolutions. For example, we may need to re-evaluate our assumptions about when to use eager vs. lazy reduction techniques when converting between formalisms.
Here at Amazon, we recently reconsidered the PhD dissertation of University of California, Berkeley, professor Sanjit Seshia in light of mallob-mono and were able to quickly (in about 2,000 lines of Rust) develop a new eager-reduction-based solver that outperforms today’s leading lazy-reduction tools on the notoriously difficult SMT-COMP bcnscheduling and job_shop benchmarks. Here we are solving SAT problems that go beyond Booleans, to involve integers, real numbers, strings, or functions. We call this SAT modulo theories, or SMT.
In the graph below we compare the performance of leading lazy SMT solvers CVC5 and Z3 to a Seshia-style eager solver based on the SAT solvers Kissat and mallob-mono on those benchmarks:
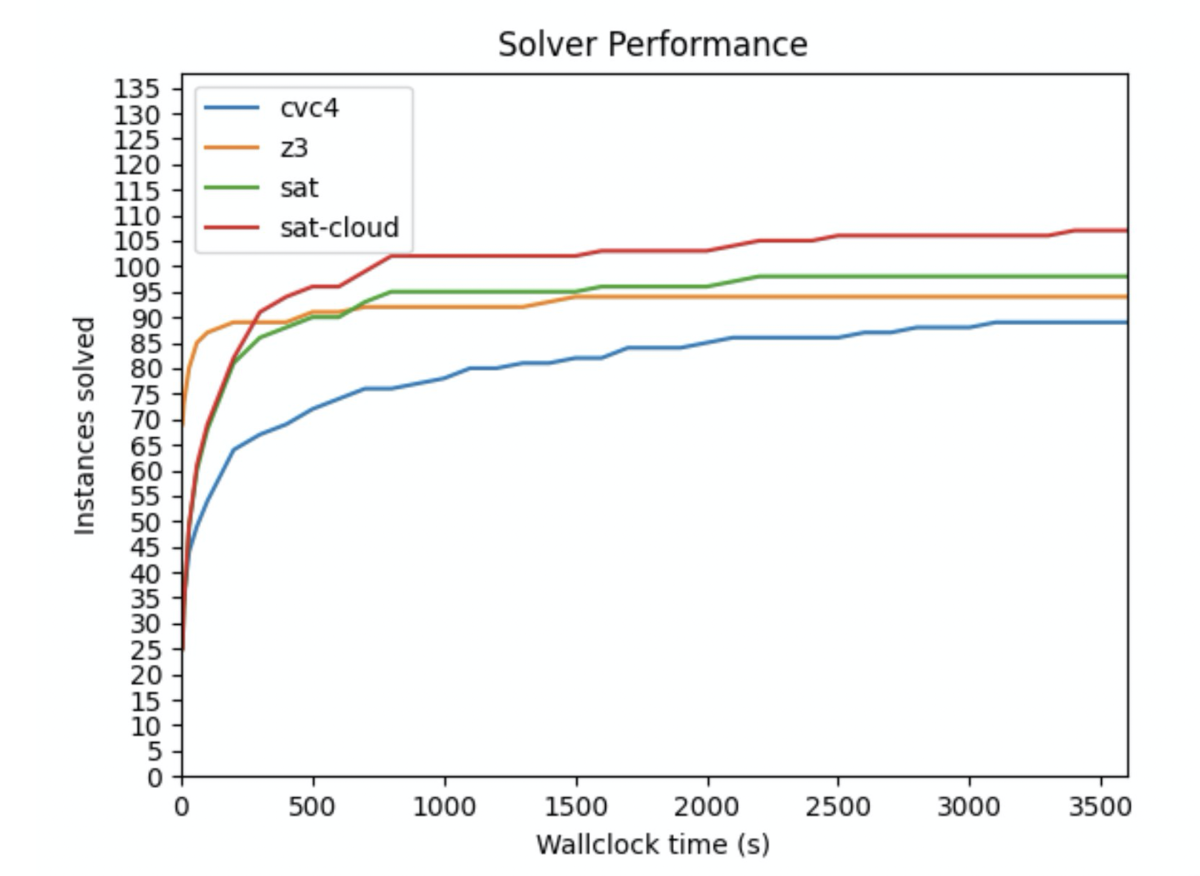
We’ve published the code for our Seshia-style eager solver on GitHub.
There are many other open questions driven by distributed proof search. For example, is there an effective lookahead-solver strategy for SMT that would facilitate cube-and-conquer? Or as the Zoncolan service does when analyzing programs for security vulnerabilities, can we memoize intermediate lemmas in a cloud database and reuse them, rather than recomputing for each query? Can Monte Carlo tree search in the cloud on past proofs be used to synthesize more-effective proof search strategies?
Another example: Reasoning about distributed systems
Recent examples of formal reasoning within AWS at the level of distributed-protocol design include a proof of S3’s recently announced strong consistency and the protocol-level proof of secrecy in AWS's KMS service. The problem with these proofs is that they apply to the protocols that power the distributed services, not necessarily to the code running on the servers that use those protocols.
Here at Amazon, we believe that automated reasoning at the level of protocol design has the greatest long-term value when the investment cost is amortized and protected via continuous integration/continuous delivery (CI/CD) integrations with the code that implements the protocols. That is, the benefit of upfront effort is often seen later, when protocol compliance proofs fail on buggy changes to implementation source code. The code doesn’t make it to production until the developers have fixed it.
Again: major perspective shifts like those resulting from successful proofs about S3 and KMS could trigger a revolution, à la Kuhn. For years, we have had tools for reasoning about distributed systems, such as TLA+ and P. But with the success of the work with S3 and KMS, it’s now clear that protocol design should be a first-class concept for engineering, with tools that support it, proactively finding errors and proving properties.
These tools should also connect to the source code that speaks the protocols by (i) constructing specifications that can be proved with existing code-level tools and (ii) synthesizing implementation code in languages such as C, Go, Rust, or Java. The tools would facilitate integration into our CI/CD, code review, and ticketing systems, allowing service teams to (iii) synthesize “runtime monitors” to exploit enterprise-level operations strength by providing telemetry about the status of a service’s conformance to a proved protocol.
Final example: Automating regulatory compliance
At the recent Computer-Aided Verification (CAV ’21) workshop called Formal Approaches to Certifying Compliance (talks recorded and available), we heard from NIST, Coalfire, Collins Aerospace, DARPA, and Amazon about the use of automated reasoning to lower the cost and the time-to-market added by regulatory compliance.
Karthik Amrutesh of the AWS security assurance team reported that automated reasoning enabled a 91% reduction in the time it took for our third-party auditor to produce evidence for checking controls. For perhaps the first time in the more than 2,500-year history of mathematical logic, we see a business use case that exploits the difference between finding proofs and checking proofs. What's the difference? Finding is usually the hard part, the creative part, the part that requires sophisticated algorithms. Finding is usually undecidable or NP-complete, depending on the context.
Meanwhile, not only is checking proofs decidable in most cases, but it’s often linear in the size of the proof. To check proofs, compliance auditors can use well-understood and trusted small solvers such as HOL-light.
Using cloud-scale automation to find the proofs lowers cost. That lets the auditor offer its services for less, saving the customer money. It also reduces the latency of audits, a major pain point for developers looking to go to market quickly.
An audit check involves constraints on the form that valid text strings can take. The set of constraints is known as a string theory, and the imposition of that theory means that audit checks are SMT problems.
From the perspective of automated-reasoning science, it becomes important to build string theory solvers that can efficiently construct easily checkable proof artifacts. In the realm of propositional satisfiability — SAT problems — the DRAT proof checker is now the standard methodology for communicating proofs. But in SMT, no such standard exists. What would a general-purpose theory-agnostic SMT format and checker look like?
Conclusion
We've come a long way from days when automated reasoning was the exclusive domain of circuit designers or aerospace engineers. Success in these early domains kicked off a virtuous cycle for the makers of the theorem provers that power automated reasoning. With applications for mainstream applications such as cloud computing, the automated-reasoning virtuous cycle is now radically accelerating. After 2,500 years of mathematical-logic research and 70+ years of automated-reasoning science, we live in a heady time. With wider adoption of and investment in automated reasoning, we are seeing economies of scale where what we can do now would have been unimaginable even two or three years ago. Welcome to the future!